Drop an Octave : Deducing Spatial Redundancy in Convolutional Neural networks with Octave Convolution
>
ALBERT : A Lite Bert For Self-Supervised Learning of Language Representations
Drop an Octave : Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution
원논문 주소 : https://arxiv.org/pdf/1904.05049.pdf
케라스 카톡 오픈톡방에서 어느분이 간단한 정보를 링크해줘서 보게되었다.
가지고 있던 아이디어와 매우 유사해 자세히 보기로. 물론 큰그림만…
Abstract
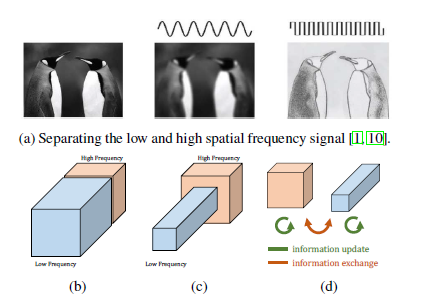
- 이미지를 주파수로 변환시 높은 주파수는 세부적인 디테일을, 낮은 주파수는 전체적인 구조를 인코딩한다.
- 그리고 컨볼루션의 피쳐맵은 주파수변환시의 베이스이미지 개념과 거의 일치함
- 그러므로 피쳐맵을 주파수별로 분해하여 낮은 주파수부분의 연산시에 메모리와 Flops를 감소시키는 OctConv라는 구조를 제안
- 전체적인 모델 아키텍쳐 구조를 수정할 필요가 없으며, 피쳐맵의 잉여분을 줄여주고 직교적이게 만들어줌
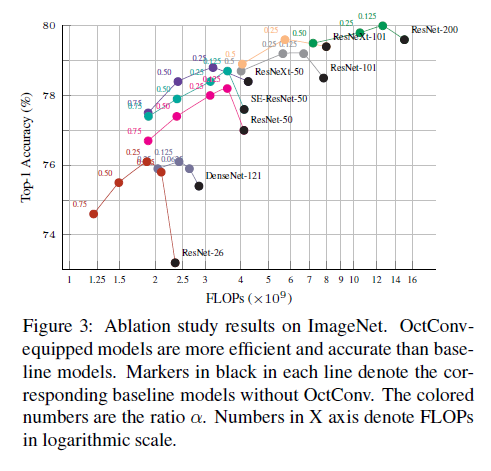
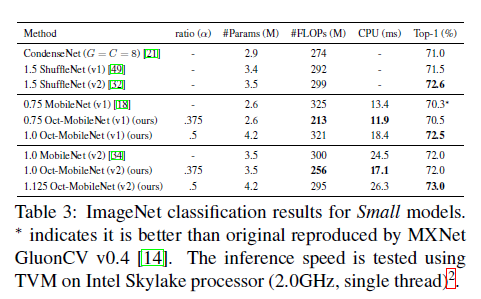
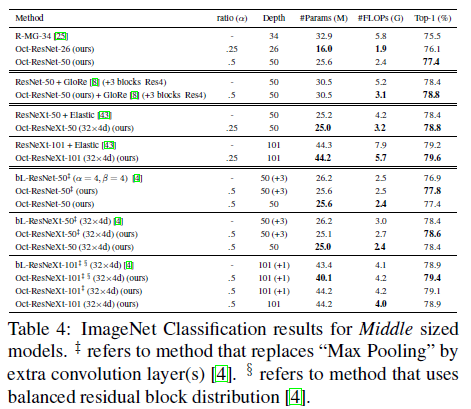
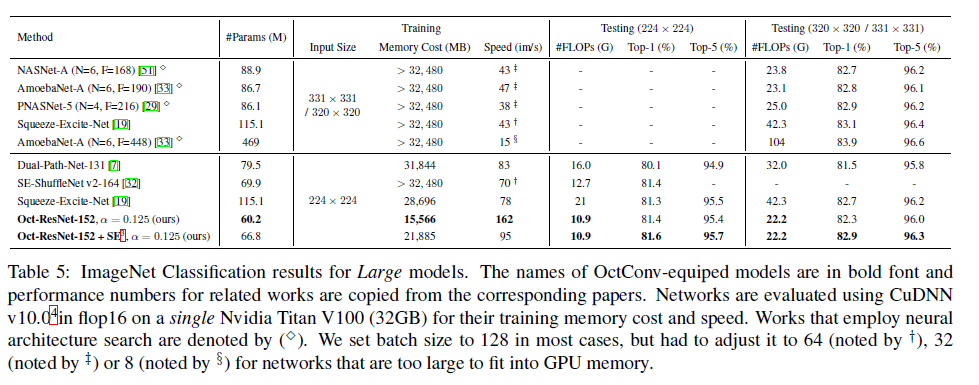
- 여러가지 모델에서 이것으로 교체하는것만으로 많은 연산량 감소와 높은 정확도를 얻었음
Method
Octave Feature Representation
- Octave : 공간차원을 두배단위로 분할 분할하는것
- 공간 중복성 감소를위하여 피쳐맵의 주파수에 따라 두가지 그룹으로 나눔
- $X\in \mathbb{R}^{c \times h\times w}$ : 입력피쳐
- $c$차원을 따라 $X = {X^H, X^L}$ 로 분해
- $X^H \in\mathbb{R}^{(1-\alpha)c\times h\times w}$
- $X^L \in\mathbb{R}^{\alpha c\times h/2\times w/2}$
- 저주파 부분으로 공간차원상에서 변화가 느림
- 피쳐맵의 크기가 고주파의 절반으로 정의됨
- $\alpha \in [0,1]$
- 전체에서 저주파의 비율
Octave Convolution
- 옥타브 방식은 중복성이 감소되고 더 압축적이지만 공간해상도 차이로 기존의 ConvNet에선 사용이 불가능.
- 가장 Naive한 방법은 원래의 해상도로 Upsampling 후 원래로 변환 할수 있으나 추가적인 비용이 필요
- Vanilla Convolution
- $Y_{p,q} = \sum_{i,j\in \mathcal{N}k}
(W{i+\frac{k-1}{2},j+\frac{k-1}{2}})^T (X^H_{p+i,q+j})$
- $k$, 커널 사이즈, $\mathcal{N}_k$ : ${-\frac{k-1}{2}}$ 부터 $\frac{k-1}{2}$ 까지의 정수, $p,q$ : 피쳐맵에서의 현재 위치
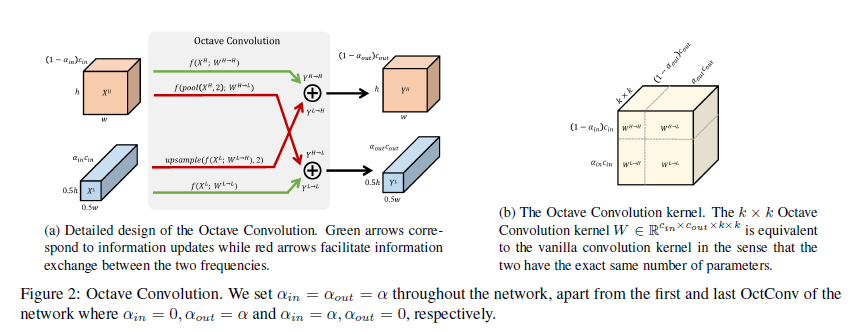
- Octave Convolution
- 출력을 $Y = {Y^H, Y^L}$ 라고 할때 컨볼루션 연산은 앞레이어 전체 채널에서 영향을 받으므로 아래 식으로 표현가능
- $Y^H = Y^{H \to H} + Y^{L \to H}, Y^L = Y^{H \to L} + Y^{L \to L}$
- 여기서 같은 그룹으로의 이동은 주파수내 업데이트로, 다른 이동은 주파수간 통신으로 생각 할 수 있음.
- 마찬가지로 가중치도 위처럼 분해가 가능
- $W^H = [W^{H \to H}, W^{L \to H}], W^L = [W^{H \to L}, W^{L \to L}]$
- 고주파에서의 처리
- $Y^H_{p,q} = Y^{H\to H}{p,q} + Y^{L\to H}{p,q}
= \sum_{i,j\in \mathcal{N}k}
(W^{H\to H}{i+\frac{k-1}{2},j+\frac{k-1}{2}})^T (X^H_{p+i,q+j}) \+
\sum_{i,j\in \mathcal{N}k}
(W^{L\to H}{i+\frac{k-1}{2},j+\frac{k-1}{2}})^T
(X^{L}_{(\lfloor\frac{p}{2}\rfloor+i),(\lfloor\frac{q}{2}\rfloor+j)})$
- 고주파의 피쳐맵에선 주파수간 통신은 컨볼루션 후 업샙플링
- 저주파에서의 처리
- $Y^L_{p,q} = Y^{L\to L}{p,q} + Y^{H\to L}{p,q}
= \sum_{i,j\in \mathcal{N}k}
(W^{L\to L}{i+\frac{k-1}{2},j+\frac{k-1}{2}})^T (X^L_{p+i,q+j}) \+
\sum_{i,j\in \mathcal{N}k}
(W^{H\to L}{i+\frac{k-1}{2},j+\frac{k-1}{2}})^T
(X^{H}_{(2p+0.5+i),(2q+0.5+j)})$
- Dilated Convolution(중심이동의 경향이 있음) 대신 평균 풀링을 사용하고 그후 컨볼루션 실행
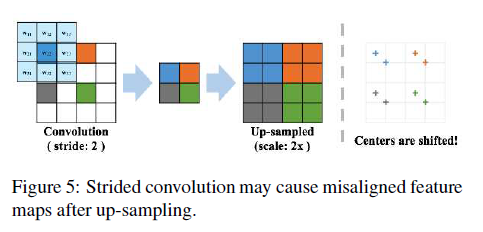
- 3.2 마지막부분에 대한 해석 필요
Implementation Details
4. Experiental Evaluation